本文共 2285 字,大约阅读时间需要 7 分钟。
图2.9显示了使用式(2.51)以0.2°增量计算的相对RCS,条件是以10 GHz的频率在距离目标中心10 km处进行观测。
Figure 2.9 shows therelative RCS, computed at 0.2° increments using Eq. (2.51), which results whenthis target is viewed 10 kmfrom its center at a frequency of 10 GHz.
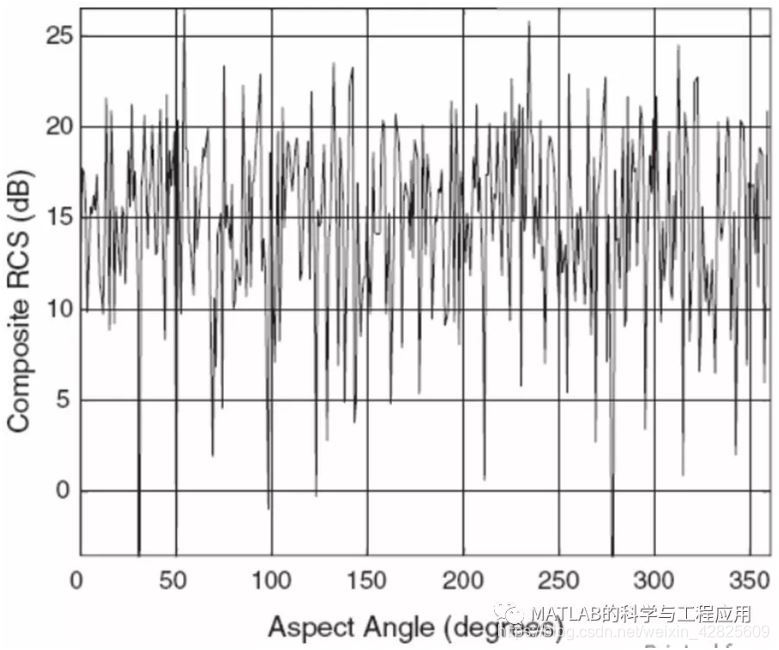
Figure 2.9. 图2.8中的复杂目标在10 km距离和10 GHz雷达频率下的相对RCS。Relative RCS of the complex targetof Fig. 2.8 at a range of 10 kmand radar frequency of 10 GHz.
该动态范围与简单的哑铃目标特征相似,但内部波瓣结构更为复杂。
The dynamic range is similar to that of thesimple dumbbell target, but the lobing structure is much more complicated.
即使是中等复杂度的目标,雷达散射截面随雷达频率和目标视线角的复杂变化也会导致对雷达横截面的统计描述。
The complicatedvariation of RCS with radar frequency and target aspect angle observed for evenmoderately complex targets leads to the use of a statistical description forradar cross section (Levanon, 1988; Nathanson, 1991; Skolnik, 2001).
这意味着单个分辨率单元内散射体的RCS值σ被视为具有指定概率密度函数(PDF)的随机变量。
This means that theRCS σ of the scatterers within a single resolution cell is considered to be arandom variable with a specified probability density function (PDF).
平均或中值雷达散射截面通常用于雷达距离方程的计算,但雷达探测概率计算需要完整的PDF信息,如第6章所示。
The mean or medianRCS is typically used for radar range equation calculations, but the full PDFis needed for detection probability calculations, as will be seen in Chap. 6.
可以采用多种PDF中的一种用于描述不同目标RCS的统计行为。
One of a variety ofPDFs is used to describe the statistical behavior of the RCS for differenttargets.
首先考虑一个由大量单个散射体组成的目标(类似于图2.8),每个散射体都有自己固定的RCS,并且在空间中随机分布。
Consider first atarget consisting of a large number of individual scatterers (similar to thatof Fig. 2.8), each with its own individual but fixed RCS and randomlydistributed in space.
由于其对距离变化的高灵敏度,各种散射体的回波相位可以假定为均匀分布在(0, 2π]上的随机变量。
Because of its highsensitivity to small range changes, the phase of the echoes from the variousscatterers can be assumed to be a random variable distributed uniformly on (0,2π].
在这种情况下,中心极限定理保证了复合回波的实部和虚部可以假设为具有相同方差α2的独立零均值高斯随机变量。
Under thesecircumstances, the central limit theorem guarantees that the real and imaginaryparts of the composite echo can each be assumed to be independent, zero meanGaussian random variables with the same variance, say α2 (Papoulisand Pillai, 2001; Beckmann and Spizzichino, 1963).
——本文译自Mark A. Richards所著的《Fundamentals of Radar Signal Processing(Second edition)》
更多精彩文章请关注微信号:
转载地址:http://qnlp.baihongyu.com/